1 Answer

Fayilt · Answer 1 · 2020-01-18T06:10:41+0000

Start with the equation

ax^2+bx+c=0

Factor
from the first two terms:

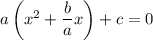
$a\left(x^2+\frac bax\right)+c=0$

Complete the square; do this by adding an appropriate constant to
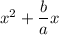$x^2+\frac bax$ to form a perfect square trinomial. Recall that

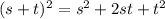
(s+t)^2=s^2+2st+t^2

So here we have

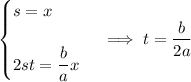
$\begin{cases}s=x\\\\2st=\frac ba x\end{cases}\implies t=\frac b{2a}$

and we have to add
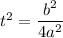t^2=(b^2)/(4a^2) to make the perfect square. But we also have to subtract this same constant to preserve equality:

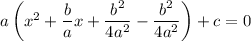
$a\left(x^2+\frac bax+(b^2)/(4a^2)-(b^2)/(4a^2)\right)+c=0$

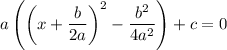
$a\left(\left(x+\frac b{2a}\right)^2-(b^2)/(4a^2)\right)+c=0$

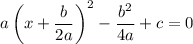
$a\left(x+\frac b{2a}\right)^2-(b^2)/(4a)+c=0$

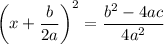
$\left(x+\frac b{2a}\right)^2=(b^2-4ac)/(4a^2)$

Now we can take the square root and solve for
:

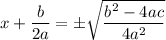
$x+\frac b{2a}=\pm\sqrt{(b^2-4ac)/(4a^2)}$

$x=-\frac b{2a}\pm\sqrt{(b^2-4ac)/(4a^2)}$

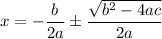
$x=-\frac b{2a}\pm(√(b^2-4ac))/(2a)$

You should recognize this formula...

Please log in or register to add a comment.