Answer:
Four
Explanation:
We have the expression
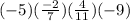 .
.
Now, four different students have applied different properties to rewrite the expression above.
1. Mitul used commutative property i.e. ab = ba
So,
![[(-5)((-2)/(7))][((4)/(11))(-9)]](https://img.qammunity.org/2020/formulas/mathematics/middle-school/wkx4fxwgnoad9fjrbgoq0pyvvw179r4y8c.png) =
=
![[((-2)/(7))(-5)][(-9)((4)/(11))]](https://img.qammunity.org/2020/formulas/mathematics/middle-school/3bzxf39iyivica9wtufk3x6goqxxfd1qfj.png) .
.
2. Stacy used associative property i.e. a(bc) = (ab)c
Then,
![-5[(-2)/(7)((4)/(11)* -9)]](https://img.qammunity.org/2020/formulas/mathematics/middle-school/3qtqg1hwt31b671vz7d5ghtydmnq3xkuk6.png) =
=
![-5[((-2)/(7)* (4)/(11))(-9)]](https://img.qammunity.org/2020/formulas/mathematics/middle-school/hhqvs1yj912td5tzk17okccpgh2bk0yuz1.png)
3. Tom used associative property followed by commutative property
Thus,
![-5[(-2)/(7)((4)/(11)* -9)]](https://img.qammunity.org/2020/formulas/mathematics/middle-school/3qtqg1hwt31b671vz7d5ghtydmnq3xkuk6.png) =
=
![-5[((-2)/(7)* (4)/(11))(-9)]](https://img.qammunity.org/2020/formulas/mathematics/middle-school/hhqvs1yj912td5tzk17okccpgh2bk0yuz1.png) =
=
![-5[((4)/(11)* (-2)/(7))(-9)]](https://img.qammunity.org/2020/formulas/mathematics/middle-school/wu84vl7mqw7kcmz4dvcuk2tvma9ulivsg3.png)
4. Walt used commutative property followed by associative property
So,
![[(-5)((-2)/(7))][((4)/(11))(-9)]](https://img.qammunity.org/2020/formulas/mathematics/middle-school/wkx4fxwgnoad9fjrbgoq0pyvvw179r4y8c.png) =
=
![[((-2)/(7))(-5)][(-9)((4)/(11))]](https://img.qammunity.org/2020/formulas/mathematics/middle-school/3bzxf39iyivica9wtufk3x6goqxxfd1qfj.png) =
=
![((-2)/(7))[(-5* -9)((4)/(11))]](https://img.qammunity.org/2020/formulas/mathematics/middle-school/1tvbbo9sq7g0yyrqd0vkuhsfh42crv0srd.png) =
=
![((-2)/(7))[(-5)(-9* (4)/(11))]](https://img.qammunity.org/2020/formulas/mathematics/middle-school/sgjgnvwasxxjs82jfju8g9hqtth46cexxg.png) .
.
Hence, we see that all the four students have rewritten the expressions equivalent to the original expression.