Question

Point A is located at (3, 6) and point B is located at (10,−2) .

What are the coordinates of the point that partitions the directed line segment AB⎯⎯⎯⎯⎯ in a 1:3 ratio?



Enter your answer, as decimals, in the boxes.

(
,
)

Answer 1

(4.75, 4)

Explanation:

I took the test

Answer 2

(4.75, 4)

Explanation:

We are to find the coordinates of the point that partitions the directed line segment AB in 1:3 ration.

For this, we will use the following formula:

`x = x_1 + k(x_2 - x_1)` ,
`y = y_1 + k(y_2-y_1)`

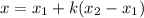where
`k` is the ratio of the first segment to the whole line segment so in this case, it will
`(1)/(4)`.

So substituting the given values in the above formula to find the coordinates:

`x = 3 + \frac {1}{4} (10-3) = 4.75`

`y = 6 + (1)/(4) (-2-6) = 4`

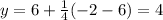
Therefore, the coordinates of the point that partitions the directed line segment AB in a 1:3 ratio are (4.75, 4).