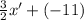Answer:
Answer: the equation is y'=
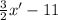
Explanation:
A line is given whose equation is given as
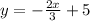 ------(1)
------(1)
and we have to find the equation of another line which is perpendicular to this.
Let the equation of the line be y'=mx'+c------(2)
This line passes through a point (8,1) so we put the values of x & y in the equation.
⇒ 1 = m×8+c
⇒ 8m+c = 1------(3)
We know that if two lines are perpendicular to each other then multiplication of their slopes is equal to (-1).
Therefore m×
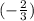 =(-1)
=(-1)
⇒
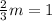
⇒m=

Now we put the value of m in equation (3) to get the value of c
8×
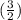 +c = 1
+c = 1
12+c=1
c = (-11)
Therefore the equation will be y'=