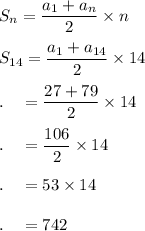Question

PLEASE HELP ASAP!!! CORRECT ANSWER ONLY PLEASE!!!

The number of people that enter a contest the first day is 27. 31 people enter the second day and 35 enter on the third day. This pattern continues and the contest lasts 14 days.

What is the total number of people that enter the contest?

Answer 1

Hello there,

The number of people that enter a contest the first day is 27. 31 people enter the second day and 35 enter on the third day. This pattern continues and the contest lasts 14 days.

What is the total number of people that enter the contest?

Answer: 742

Answer 2

Answer: 742

Explanation:

The given sequence {27, 31, 35, ... } provides the following information:

• the first term (a₁) = 27
• the difference (d) = 4

We can use the information above to find the explicit rule of the sequence:

`a_n=a_1+d(n-1)\\.\quad =27+4(n-1)\\.\quad =27+4n-4\\.\quad =23+4n`

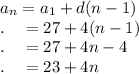
We can use the explicit rule to find the 14th term (a₁₄)

`a_n=23+4n\\a_(14)=23+4(14)\\.\quad =23+56\\.\quad =79`

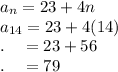
Next, we can input the first and last term of the sequence into the Sum formula:

`S_n=(a_1+a_n)/(2)* n\\\\S_(14)=(a_1+a_(14))/(2)* 14\\\\.\quad =(27+79)/(2)* 14\\\\.\quad =(106)/(2)* 14\\\\.\quad =53* 14\\\\.\quad =742`