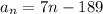Question

What is the explicit rule for the sequence? −182,−175,−168,−161,...

Answer 1

an = 7n − 189

Hope this helps :)

Answer 2

`a_n = 7n - 189`

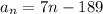
Explanation:

The given sequence is -182, -175, -168, -161, ...

It is an arithmetic sequence, because the difference between the successive term is the same constant.

d = -175 - (-182) = -175 +182 = 7

d = -168 - (-175) = -168 + 175 = 7

So the difference (d) = 7

The first term is
`a_1 = -182`

The explicit formula of an arithmetic sequence is
`a_n = a_1 + (n -1)d`

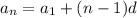
Now plug in a_1 = -182 and d = 7

`a_n = -182 + (n-1)7`

`a_n = -182 + 7n - 7`

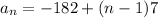
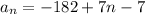
Simplify the like terms

`a_n = 7n - 189`