Question

Who can help me with my work

Answer 1

1. Answer:
`y=(3)/(4)x-3`
`m=(3)/(4)`
`b=-3`

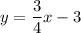
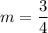
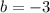
Explanation:

The slope-Intercept form is: y = mx + b

• m is the slope
• b is the y-intercept

3x - 4y = 12

-4y = -3x + 12 subtracted 3x from both sides

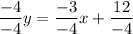`(-4)/(-4)y=(-3)/(-4)x+(12)/(-4)` divided both sides by -4

`y=(3)/(4)x-3`

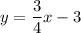
• m =
  `(3)/(4)`
• b = -3

*************************************************************************************

2. Answer:
`y=(1)/(3)x-5`
`m=(1)/(3)`
`b=-5`

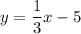
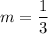
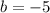
Explanation:

The slope-Intercept form is: y = mx + b

• m is the slope
• b is the y-intercept

x - 3y = 15

-3y = -x + 15 subtracted x from both sides

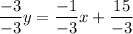`(-3)/(-3)y=(-1)/(-3)x+(15)/(-3)` divided both sides by -3

`y=(1)/(3)x-5`

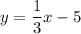
• m =
  `(1)/(3)`
• b = -5

*************************************************************************************

3. Answer: y = -5x + 9 m = -5 b = 9

Explanation:

The slope-Intercept form is: y = mx + b

• m is the slope
• b is the y-intercept

5x + 2y = y + 9

5x + y = 9 subtracted y from both sides

y = -5x + 9 subtracted x from both sides

• m = -5
• b = 9

*************************************************************************************

4. Answer:
`x=-(5)/(7)`
`x=3`

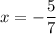
Explanation:

To solve an absolute value equation:

• isolate the absolute value expression
• split the equation into 2 equations (one positive and one negative)
• solve for each equation
• NOTE: absolute value expression cannot be equal to a negative

| 7x - 8 | = 13 isolated absolute value expression is equal to a positive

-(7x - 8) = 13 +(7x - 8) = 13 separated into 2 equations

7x - 8 = -13 7x - 8 = 13 divided by the +/- sign

7x = -5 7x = 21 added 8 to both sides

x =
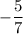`-(5)/(7)` x = 3 divided both sides by 7

*************************************************************************************

5. Answer: x = -9 x = -2

Explanation:

To solve an absolute value equation:

• isolate the absolute value expression
• split the equation into 2 equations (one positive and one negative)
• solve for each equation
• NOTE: absolute value expression cannot be equal to a negative

3| 2x + 11 | = 21 need to divide both sides by 3

| 2x + 11 | = 7 isolated absolute value expression is equal to a positive

-(2x + 11) = 7 +(2x + 11) = 7 separated into 2 equations

2x + 11 = -7 2x + 11 = 7 divided by the +/- sign

2x = -18 2x = -4 subtracted 11 from both sides

x = -9 x = -2 divided both sides by 2

*************************************************************************************

6. Answer: No solution

Explanation:

To solve an absolute value equation:

• isolate the absolute value expression
• split the equation into 2 equations (one positive and one negative)
• solve for each equation
• NOTE: absolute value expression cannot be equal to a negative

-2| x + 7 | - 3 = 13 need to add 3 to both sides

-2| x + 7 | = 16 need to divide both sides by -2

| x + 7 | = -8 isolated absolute value expression is equal to a negative

It is not possible for a positive (absolute value) to be equal to a negative so there is no solution.