Question

Find cos if sin = -2/3 and falls in quadrant 3.

a. cos = 5 squared/3
b. non of these
c. cos= (2)5 squared/5
d. cos = - 5 squared/3
c. cos = - (2)5 squared/5

Answer 1

`cos x = (√(5) )/(3)`

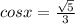
Explanation:

We are given sin = -2/3 which falls in the 3rd quadrant and we are to find the value of cos with the help of this given information.

We know that,
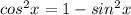`cos^2x= 1- sin^2x`. therefore we will square the given value of sin:

`sin = -(2)/(3)`

`sin^2x = (sin = -(2)/(3) )^2`

`sin^2x= (4)/(9)`

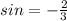
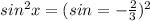
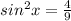
Now substituting this value of
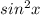`sin^2x` in the above mentioned formula to get:

`cos^2x= 1- (4)/(9)`

`cos^2x=(5)/(9)`

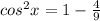
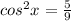
Taking square root on both the sides to get:

`√(cos^2x) = \sqrt{(5)/(9) }`

`cos x = (√(5) )/(3)`

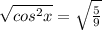
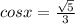
Therefore,
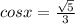`cos x = (√(5) )/(3)` since it is positive in the 3rd quadrant.

Answer 2

a.
`cos \ x=(√(5) )/(3)`.

Explanation:

Given sin x= -2/3.

Squaring both sides, we get

`sin^2x=(-(2)/(3))^2`

`sin^2x=(4)/(9)`.

We know,

`cos^2x= 1-sin^2x`

Plugging the value of
`sin^2x`

`cos^2x= 1-(4)/(9)`

`cos^2x= (1)/(1) -(4)/(9)`

`cos^2x= (9)/(9) -(4)/(9)`

`cos^2x= (9-4)/(9)`

`cos^2x= (5)/(9)`

Taking square root on both sides, we get

`√(cos^2x) = \sqrt{(5)/(9)}`

`cos \ x=(√(5) )/(3)`.

Note: In 3rd qadrant cos is positive.

Therefore,
`cos \ x=(√(5) )/(3)`.