Question

Find the number of sides of a regular polygon given the measure of one interior angle.

Answer 1

Answer: Number of sides of regular polygon is 2.

But with two sides it can't form polygon.

Explanation:

Since we have given that

Measure of one interior angle is given by

`9.144\textdegree`

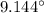
so, As we know that to get an exterior angle , we will use "Linear pair":

Let exterior angle be x.

`x+9.144\textdegree=180\textdegree\\\\x=180\textdegree-9.144\textdegree\\\\x=170.856\textdegree`

Now, we know the formula for " Number of sides ":

`\text{Number of sides }=(360)/(x)\\\\\text{Number of sides }=(360)/(170.856)\\\\\text{Number of sides }=2.1\\\\\text{but number of sides can't be in decimal.So,}\\\\\text{Number of sides }=2`

Hence, Number of sides of regular polygon is 2.

But with two sides it can't form polygon.