Question

It is given that parallelogram JKLM is a rectangle and by the definition of a rectangle, ∠JML and ∠KLM are right angles. ∠JML≅∠KLM because . JM⎯⎯⎯⎯⎯≅KL⎯⎯⎯⎯⎯ because , and ML⎯⎯⎯⎯⎯⎯≅ML⎯⎯⎯⎯⎯⎯ by the reflexive property of congruence. By the , △JML≅△KLM . Because , JL⎯⎯⎯⎯≅MK⎯⎯⎯⎯⎯⎯ .

Answer 1

Explanation:

It is given that the parallelogram JKLM is a rectangle and by the definition of rectangle, ∠JML and ∠KLM are right angles, ∠JML ≅∠KLM because all right angles are congruent.

\overline{JM}≅\overline{KL} because opposite sides of a parallelogram are congruent, and \overline{ML}≅\overline{ML} by the reflexive property of congruence. By the SAS congruence postulate, ΔJML≅ΔKLM, because corresponding parts of congruent triangles are congruent, \overline{JL}≅\overline{MK}.

Answer 2

• all right angles are congruent.
• opposite sides of a parallelogram are congruent
• SAS congruence postulate
• corresponding parts of congruent triangles are congruent

Explanation:

Given : Parallelogram JKLM is a rectangle and by the definition of rectangle,
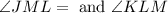`\angle{JML}=\text{ and }\angle{KLM}` are right angles,

Since all interior angles of rectangle are right angle.

then
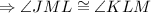`\Rightarrow\angle{JML}\cong\angle{KLM}`, because all right angles are congruent.

Also, opposite sides of a parallelogram are congruent.

`\overline{JM}\cong\overline{KL}`

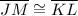
and
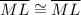`\overline{ML}\cong\overline{ML}` by the reflexive property of congruence.

Now, by the SAS congruence postulate,

`\triangle{JML}\cong\triangl{KLM}`,

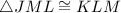Since corresponding parts of congruent triangles are congruent, ∴

`\overline{JL}\cong\overline{MK}`

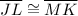
• The SAS postulate says that if two sides and the included angle of a triangle are congruent to two sides and the included angle of another triangle then the two triangles are congruent.