Answer:
Second graph is the correct option as the solution is
 and
and
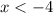 .
.
Explanation:
We are given the inequality,
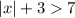 .
.
On simplifying the inequality, we have,
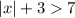
implies
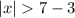
i.e.
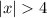
Since, we know,
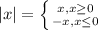
So, we get,
 and
and
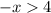
i.e.
 and
and
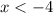
Thus, the solution is the set of numbers less than -4 and greater than 4.
Hence, the second graph is the correct option.