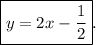Question

Find the ninvertical asymptotes of

`h(x) = \frac{(4{x}^(2) + 5x - 2 )}{ 2x + 3}`

Answer 1

`\boxed{y=2x-(1)/(2)}.`

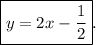
Explanation:

We may start by noticing that
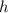`h` doesen't have horizontal asymptotes:

`\lim\limits_(x\to\pm\infty) h(x) = \lim\limits_(x\to\pm\infty) (4x^2+5x-2)/(2x+3) \overset{(\infty)/(\infty)}{=} \lim\limits_(x\to\pm\infty) (8x+5)/(2) = \pm\infty,`

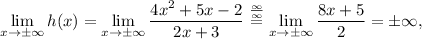
where we have used L'Hôpital's rule. Let's now check if it has any oblique asymptotes of the form
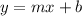`y = mx+b`, with:

`m = \lim\limits_(x\to\pm\infty)(h(x))/(x) \quad\textrm{and}\quad b = \lim\limits_(x\to\pm\infty) (h(x)-mx),`

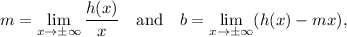
provided that the limits exist. Let's compute them using L'Hôpital's rule:

`m = \lim\limits_(x\to\pm\infty) (h(x))/(x) = \lim\limits_(x\to\pm\infty) (4x^2+5x-2)/(x(2x+3))= \lim\limits_(x\to\pm\infty) (4x^2+5x-2)/(2x^2+3x)\overset{(\infty)/(\infty)}{=}\\\\= \lim\limits_(x\to\pm\infty) (8x+5)/(4x+3) \overset{(\infty)/(\infty)}{=} \lim\limits_(x\to\pm\infty) (8)/(4) = 2`

`b=\lim\limits_(x\to\pm\infty) (h(x) - 2x) = \lim\limits_(x\to\pm\infty) \left((4x^2+5x-2)/(2x+3) - 2x\right) =\\\\=\lim\limits_(x\to\pm\infty) (4x^2+5x-2-4x^2-6x)/(2x+3) =\lim\limits_(x\to\pm\infty) (-x-2)/(2x+3) \overset{(\infty)/(\infty)}{=} \lim\limits_(x\to\pm\infty) (-1)/(2)= -(1)/(2).`

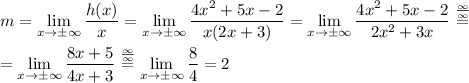
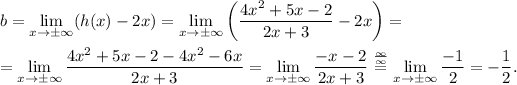
So we conclude that
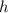`h` has an oblique asymptote, for
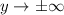`y\to\pm\infty`, given by the equation:

`\boxed{y=2x-(1)/(2)}.`