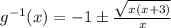Answer:
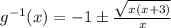
Explanation:
Given :
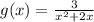
To find :
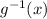
Solution :
We have given the function,
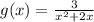
To find inverse let y=g(x)
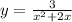
Replace the value of x and y,
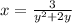
Solve for y,
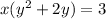
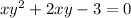
Solve by quadratic formula,
i.e. The equation
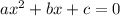 has solution
has solution
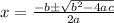
On comparing, a=x , b=2x , c=-3
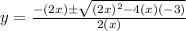
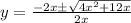
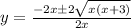
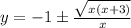
Therefore, The inverse of g(x) is