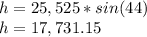Question

a straight road to the top of a mountain is 25525 feet long and makes a 44 degree angle of elevation from sea level. determine the hight of the mountain.

Answer 1

Answer: 17,731.15 feet.

Explanation:

1. You know that the straight road to the top of a mountain is 25,525 feet long and makes an angle of elevation of 44 degrees from sea level.

2. Therefore, you can draw a right triangle like the is shown in the figure attached, where h is the height and the angle α is the angle of elevation of 44 degrees from sea level.

3. You can calculate the height h as following:

`sin\alpha=(opposite)/(hypotenuse)\\`

`\alpha=44`°

`opposite=h\\hypotenuse=25,525`

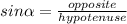
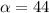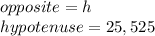
4. Solve for h. Then, you obtain the following result:

`h=25,525*sin(44)\\h=17,731.15`