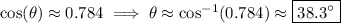The horizontal component of the tension in the string is a centripetal force, so by Newton's second law we have
• net horizontal force
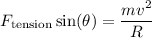
where
 ,
,
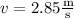 , and
, and
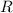 is the radius of the circular path.
is the radius of the circular path.
As shown in the diagram, we can see that
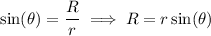
where
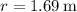 , so that
, so that
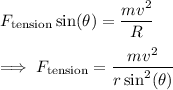
The vertical component of the tension counters the weight of the mass and keeps it in the same plane, so that by Newton's second law we have
• net vertical force

Solve for
 :
:
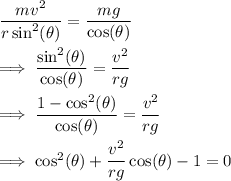
Complete the square:

Plugging in the known quantities, we end up with

The second case has no real solution, since
 for all
for all
 . This leaves us with
. This leaves us with