Note that

Taking square roots on both sides, we have
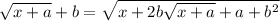
Now suppose
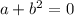 and
and
 . Then
. Then
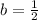 and
and
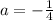 , so we can simply write
, so we can simply write
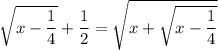
This means
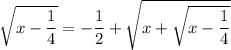
and substituting this into the root expression on the right gives
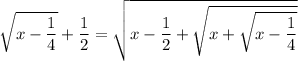
and again,
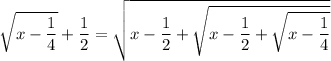
and again,

and so on. After infinitely many iterations, the right side will converge to an infinitely nested root,
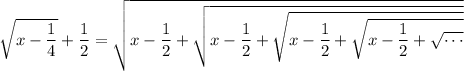
We get the target expression when
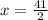 , since
, since
 , which indicates the infinitely nested root converges to
, which indicates the infinitely nested root converges to
