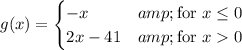
Since
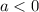 , we have
, we have
 .
.
Since
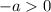 ,
,
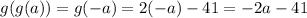 .
.
Meanwhile,
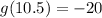 , and
, and
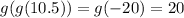 , and
, and
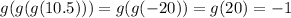 .
.
So we want to find
 such that
such that
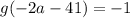 .
.
Suppose
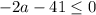 , which happens if
, which happens if
 . Then
. Then
 , so that
, so that
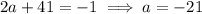 . But -21 is smaller than -20.5, so there's a contradiction.
. But -21 is smaller than -20.5, so there's a contradiction.
This means we must have
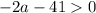 , which occurs for
, which occurs for
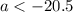 . Then
. Then
 , so that
, so that
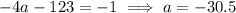 .
.