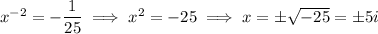Given
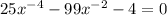
consider substituting
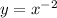 to get a proper quadratic equation,
to get a proper quadratic equation,
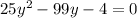
Solve for
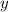 ; we can factorize to get
; we can factorize to get
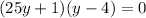
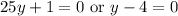
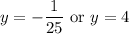
Solve for
 :
:
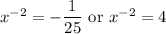
The first equation has no real solution, since
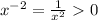 for all non-zero
for all non-zero
 . Proceeding with the second equation, we get
. Proceeding with the second equation, we get
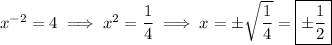
If we want to find all complex solutions, we take
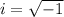 so that the first equation above would have led us to
so that the first equation above would have led us to