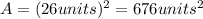Answer:
Explanation:
1. To solve this problem you must apply the formula for calculate the area of a square, which is:
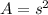
Where s is the lenght of a side of the square.
2. By definition, the sides of the square have equal lenghts. You can calculate the lenght of a side by calculating the distance between two vertices of the aquare:
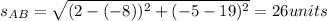
Where
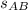 is the lenght of the side AB.
is the lenght of the side AB.
3. The area is: