Question

What is the period of `y = 1+ tan((1)/(2)x)`?

A. `(1)/(2)`
B. π
C. 2π
D. 1

Answer 1

C.
`2\pi`

Explanation:

We have been given a trigonometric function
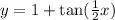`y=1+\text{tan}((1)/(2)x)`. We are asked to find period of our given function.

We know that period of a tangent function is form
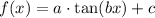`f(x)=a\cdot \text{tan}(bx)+c`, is
`\text{Period}=(\pi)/(|b|)`.

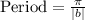We can rewrite our given function as:

`y=\text{tan}((1)/(2)x)+1`

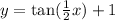
We can see that value of b is
`(1)/(2)` for our given function.

`\text{Period}=(\pi)/((1)/(2))`

Using fraction rule
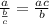`(a)/((b)/(c))=(ac)/(b)`, we will get:

`\text{Period}=(2\pi)/(1)`

`\text{Period}=2\pi`

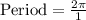
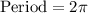
Therefore, period of our given function is
`2\pi` and option C is the correct choice.

Answer 2

ANSWER

C. 2π

EXPLANATION

The given function is


`y = 1 + \tan( (1)/(2)x )`

The period of the tangent function is given by


`T = (\pi)/( B )`

where B is the coefficient of the argument of the tangent function.

This implies that,


`B = (1)/(2)`

Hence, the period of the given function is,


`T = (\pi)/( (1)/(2) )`

This simplifies to,


`T = 2\pi`

The correct answer is option C.