Answer:
The
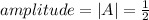 ,
,
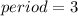 and
and
 .
.
Explanation:
The given function is
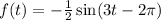 .... (1)
.... (1)
The general form of sine function is
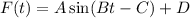 ....(2)
....(2)
where, |A| is the amplitude, B is period, D is the vertical shift (up or down), and C/B is used to find the phase shift.
On comparing (1) and (2), we get
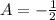
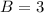
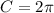
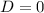
So,
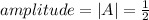
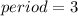

Therefore
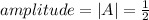 ,
,
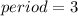 and
and
 .
.