Question

Graph g(x) = 5|x-6| + 2

Answer 1

Answer + Step-by-step explanation:

`f(x) = 5|x-6|+2 = \begin{cases}5\left( x-6\right) +2&if\ x\geq 6\\ 5\left( 6-x\right) +2 &if\ x\leq 6\end{cases}`

`\Longrightarrow f(x) = \begin{cases}5x-30+2&if\ x\geq 6\\ 30-5x +2 &if\ x\leq 6\end{cases}`

`\Longrightarrow f(x) = \begin{cases}5x-28&if\ x\geq 6\\ -5x +32 &if\ x\leq 6\end{cases}`

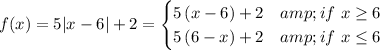
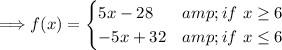
case 1: x ≥ 6 → f(x) = 5x - 28

5(6) - 28 = 30 - 28 = 2

Then

the point A(6 ,2) lie on the graph (line) of f

5(7) - 28 = 35 - 28 = 7

Then

the point B(7 ,7) lie on the graph (line) of f

Graphing :

When x ≥ 6 ,the graph of f is the ray [AB) (just connect the points A and B)

case 2: x ≤ 6 → f(x) = -5x + 32

-5(6) +32 = -30 + 32 = 2

Then

the point A(6 ,2) lie on the graph (line) of f

-5(5) +32 = -25 + 32 = 7

Then

the point C(5 ,7) lie on the graph (line) of f

Graphing :

When x ≤ 6 ,the graph of f is the ray [AC) (just connect the points A and C)