Answer:
Solutions of x are;
x = -7 + 8i and x = -7 -8i
Explanation:
Given the equation:
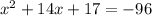
Add 96 both sides we get;
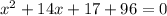
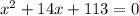
Using quadratic formula
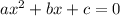 then the solution is given by:
then the solution is given by:
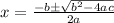
On comparing we have;
a= 1, b =14 and c =113
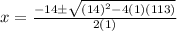
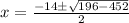
or
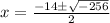
Simplify:
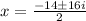 ; where i is the imaginary,
; where i is the imaginary,
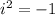
or
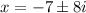
Therefore, the solution of x are; x = -7 + 8i and x = -7 -8i