Question

The polynomial x 3 + 5x 2 - ­57x -­189 expresses the volume, in cubic inches, of a shipping box, and the width is (x+3) in. If the width of the box is 15 in., what are the other two dimensions? ( Hint: The height is greater than the depth.)

Answer 1

Answer: Other two dimensions are 21 and 5.

Height = 21 in.

Depth = 5 in.

Explanation:

Since we have given that

`x^3 + 5x^2 -57x-189=0`

As we have given that

Width = x+3

That means
`x+3=0\\\\x=-3`

So, by dividing, x^3 + 5x^2 -57x-189 by x+3 we get,

`(x^3 + 5x^2 -57x-189)/(x+3)\\\\\mathrm{Divide\:the\:leading\:coefficients\:of\:the\:numerator\:}x^3+5x^2-57x-189\mathrm{\:and\:the\:divisor\:}x+3\mathrm{\::\:}(x^3)/(x)=x^2\\\\Quotient=x^2\\\\\mathrm{Multiply\:}x+3\mathrm{\:by\:}x^2:\:x^3+3x^2\\\\\mathrm{Subtract\:}x^3+3x^2\mathrm{\:from\:}x^3+5x^2-57x-189\mathrm{\:to\:get\:new\:remainder}\\\\\mathrm{Remainder}=2x^2-57x-189\\\\=x^2+(2x^2-57x-189)/(x+3)`

`\mathrm{Divide\:the\:leading\:coefficients\:of\:the\:numerator\:}2x^2-57x-189\mathrm{\:and\:the\:divisor\:}x+3\mathrm{\::\:}(2x^2)/(x)=2x\\\\\mathrm{Quotient}=2x\\\\\mathrm{Multiply\:}x+3\mathrm{\:by\:}2x:\:2x^2+6x\\\\\mathrm{Subtract\:}2x^2+6x\mathrm{\:from\:}2x^2-57x-189\mathrm{\:to\:get\:new\:remainder}\\\\\mathrm{Remainder}=-63x-189\\\\=x^2+2x+(-63x-189)/(x+3)\\\\=x^2+2x-63`

Noe, we split the quadratic equation:

`x^2+2x-63=0\\\\x^2+9x-7x-63=0\\\\x(x+9)-7(x+9)=0\\\\(x+9)(x-7)=0\\\\x=-9,7`

So, as we have given that

Width = 15

`so, x+3=15\\\\x=15-3\\\\x=12\\\\Length=x-7=12-7=5\\\\\Height = x+9=12+9=21`

So, other two dimensions are 21 and 5.

Height = 21 in.

Depth = 5 in.

Answer 2

The other two dimensions are either (x+9) or (x-7). other two dimensions are either 21 inches or 7 inches.

Explanation:

The volume is defined by the function.

`V(x)=x^3+5x^2-57x-189`

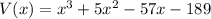
The width is (x+3).

Using synthetic or long division method divide
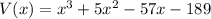`V(x)=x^3+5x^2-57x-189` by (x+3).

`V(x)=(x+3)(x^2+2x-63)`

`V(x)=(x+3)(x^2+9x-7x-63)`

`V(x)=(x+3)(x+9)(x-7)`

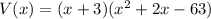
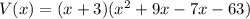
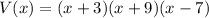
The volume of cuboid is

`V=l* b* h`

Therefore other two dimensions are either (x+9) or (x-7).

If the width is 15 inches, then

`x+3=15`

`x=12`

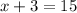
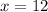
The other two dimensions are

`x+9=12+9=21`

`x-7=12-7=5`

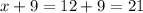
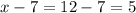
Therefore other two dimensions are either (x+9) or (x-7). other two dimensions are either 21 inches or 7 inches.