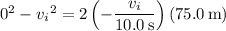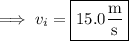Since acceleration is constant, the average and instantaneous accelerations are the same, so that

By the same token, we have the kinematic relation

where
 is final speed,
is final speed,
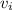 is initial speed,
is initial speed,
 is acceleration, and
is acceleration, and
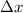 is displacement.
is displacement.
Substitute everything you know and solve for
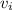 :
: