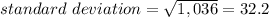Answer:
The standard deviation of the following data set is 32.2
Explanation:
step 1
Find the mean
we have
![[56,78,123,34,67,9,20]](https://img.qammunity.org/2020/formulas/mathematics/middle-school/9qgoiii7q12s4xvxchcycxx7lhkmfll496.png)
Sum the data and divided by the number of elements
![[56+78+123+34+67+91+20]/7=469/7=67](https://img.qammunity.org/2020/formulas/mathematics/middle-school/i3oe4bj80m0uv5n7l9vz4fc9eq54869slf.png)
step 2
For each number: subtract the Mean and square the result
![[(56-67)^(2),(78-67)^(2),(123-67)^(2),(34-67)^(2),(67-67)^(2),(91-67)^(2),(20-67)^(2)]](https://img.qammunity.org/2020/formulas/mathematics/middle-school/tb4e188lxk7vblz7m5c8mr1fosmflx1oaj.png)
![[121,121,3,136,1,089,0,576,2,209]](https://img.qammunity.org/2020/formulas/mathematics/middle-school/mmvzh33xxds0skeo7fvvrr8b3jbqiyty36.png)
step 3
Work out the mean of those squared differences
![[121+121+3,136+1,089+0+576+2,209]/7=1,036](https://img.qammunity.org/2020/formulas/mathematics/middle-school/uto8cwz72iqebmb3qxyijjimx0cqe516wi.png)
This value is called the "Variance"
step 4
Take the square root of the variance