Question

How are ratios, unit rates, and proportions related to slope intercept? Last question! Wil give extra points to who answers first!

Answer 1

Slope intercept form of line

y= m x + c,

If you put , c=0, the equation of line in two dimensions becomes the equation of line passing through Origin .There will be infinite number of lines for different values of m, which is slope.

So, if you will write general equation of line passing through origin:

y = m x

`m= (y)/(x)`

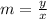
Now coming to ratios, Suppose we have to find the value of 8: 4 , it gives a finite value,
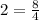`2= (8)/(4)`, so if we have to find The value of , a: b, then
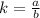`k= (a)/(b)` or , a = bk, which is equation of line if you replace b By x and a by y and k is used to represent Slope of line.

Similarly, While calculating Unit rate , we divide Distance by time or Displacement by time Taken . For example ,Representing Displacement or Distance by D and time taken by T, then We can write
`R= (D)/(T)` or can be Represented as , D= R T, which is same as equation of line if you replace D by y and T by x, as R will work as slope.

Considering Proportions, Four quantities a:b::c:d are said to be in proportion if , the two ratios are equivalent that is
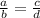`(a)/(b)=(c)/(d)`.If we Write either
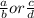`(a)/(b) or (c)/(d)` equal to t. the ratio will become , a= b t or c = d t, which is same as equation of line y=m x, if we replace b or d by x and a or c by y and t works as slope of line.