Answer:
Proof below
Explanation:
General Strategy:
- Find factors of divisor
- Use algebraic properties to reveal those factors in the given expression.
Divisibility
A number, p, is divisible by another number, d, if and only if there is some non-negative integer, n, such that n*d=p.
To prove that, 300 is divisible by 10 because, 30 is a non-negative integer, and 10*30=300.
Strategies for Divisibility by a composite number
Note that in the previous example, 10 is a composite number. This means that both one 2 and one 5 (the full list of 10s factors) had to be factored out of the 300.
In the given problem, we are to prove that the number is divisible by 14. Observe 14 is composite with factors of 2 and 7.
Properties of exponents
Since the expression is given with exponents, it will be helpful to recall a few exponent properties to algebraically manipulate the expression.
Recall the following property of exponents:
Finding a factor of 14 in the given expression
Original expression...
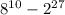
Recognizing 8 as a power of 2...
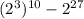
Simplifying and rewriting so that both terms are powers of 2...
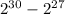
Observing that both terms have 27 twos as factors...
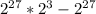
Factoring out 27 twos...
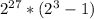
Simplifying the expression in the parenthesis:
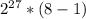

Knowing that we also need a factor of 2, use properties of exponents, and associative property of multiplication...
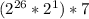
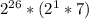
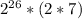

Since 2^26 is a non-negative integer, the original expression is divisible by 14.