Question

Find the sine function that is represented in the graph.

Answer 1

Choice D).
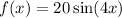`f(x)=20\sin(4x)` is correct.

Explanation:

Given function graph is sinusoidal so let's compare with formula
`f(x)=A\sin(Bx-C)+D`

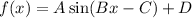
We know that amplitude is the height from the center line to the peak (or to the trough). From graph we can see that height from the center line to the peak is 20

So amplitude A=20

In that formula, period is given by
`(2\pi)/(B)`

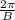
From graph we see that period is
`(\pi)/(2)`

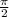
So both must be equal

`(2\pi)/(B)=(\pi)/(2)`

`(2)/(B)=(1)/(2)`

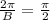
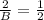
cross multiplying them gives

B=4

Clearly there is no shift so C and D are 0

Now plug these values into formula
`f(x)=A\sin(Bx-C)+D`

`f(x)=20\sin(4x-0)+0`

`f(x)=20\sin(4x)`

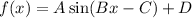
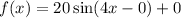
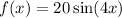
Hence choice D is correct.