Question

Describe the 2 transformations that occur when the graph of f(x) =x −−√ is transformed to the graph of g(x) = 2x√ +3 .

Answer 1

Dilation followed by Translation.

Explanation:

We have the function
`f(x)=√(x)`.

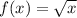The new transformed function is
`g(x)=2√(x)+3`

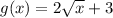
Now, the transformation applied to f(x) to obtain g(x) are:

1. Dilation - it is the transformation that changes the size/shape of the figure. It is generally of the form kf(x) where k is constant.

Since, we are dilating the given function by 2 units, the new dilated function becomes
`2√(x)`.

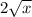2. Translation - it is the transformation that shifts the figure in any direction. When the function is shifted vertically, the general form becomes f(x)+k.

As, we see that the new dilated function is shifted 3 units upwards, the final translated function becomes
`g(x)=2√(x)+3`.

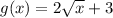Hence, the transformations applied to obtain g(x) from f(x) are Dilation followed by Translation.