Answer:
Daniel had total $70 before shopping.
Explanation:
Let us assume that Daniel had total money before shopping = $x.
He spent
 of total money on books, that is = $
of total money on books, that is = $
 of x=
of x=
 x.
x.
Remaining money with him = (x-
 x) .
x) .
And spent 1/3 of the remaining that is 1/3 of (x-2/5x) = 1/3(x-
 x) on food.
x) on food.
Money left with him = $28.
Therefore, we can setup and equation.
Money spent on books + Money spent on food + Remaining money = Total money before shopping.
Substituting above values in equation, we get
 x +
x +
 (x-
(x-
 x) + 28 = x.
x) + 28 = x.
Subtracting x-
 x =
x =
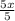 -
-
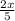 =
=
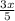 , we get
, we get
 x +
x +
 (
(
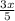 ) + 28 = x.
) + 28 = x.
Multiplying
 (
(
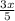 ), we get
), we get

Therefore,
 x +
x +
 +28=x
+28=x
 x +28 =x.
x +28 =x.
Subtracting
 on both sides, we get
on both sides, we get
 x + 28-
x + 28-
 x =x-
x =x-
 x
x
28 =
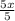 -
-
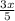
28 =
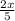 .
.
Multiplying both sides by 5, we get
28×5 = 5×
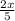 .
.
140 =2x.
Dividing both sides, by 2, we get
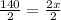
x=70.
Therefore, Daniel had total $70 before shopping.