A countries population in 1991 was 147 million. In 1998 it was 153 million. Estimate the population in 2017 using the exponential growth formula round your answer to the nearest…

Question

asked Feb 23, 2020 194k views

1 Answer

John Robins · Answer 1 · 2020-02-28T12:34:00+0000

Answer:

The population in 2017 is 171 million

Explanation:

Let's assume population starts from 1991

so,

initial population is 147 million

so,
A=147

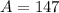
we can use formula

P=Ae^(kt)

we can plug A=147

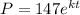
P=147e^(kt)

In 1998:

t=1998-1991=7

P=153

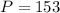
now, we can plug these values into formula and find k

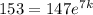
153=147e^(7k)

Divide both sides by 147

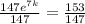
(147e^(7k))/(147)=(153)/(147)

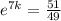
e^(7k)=(51)/(49)

$\ln \left(e^(7k)\right)=\ln \left((51)/(49)\right)$

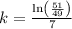
$k=(\ln \left((51)/(49)\right))/(7)$

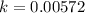
k=0.00572

now, we can plug it back

and we get

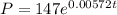
P=147e^(0.00572t)

In 2017:

t=2017-1991=26

we can plug it and find P

P=147e^(0.00572* 26)

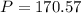
P=170.57

So,

The population in 2017 is 171 million