Question

A soccer ball is kicked into the air from the ground. If the ball reaches a maximum height of 25 ft and spends a total of 2.5 s in the air, which equation models the height of the ball correctly? Assume that acceleration due to gravity is –16 ft/s2. h(t) = at2 + vt + h0

Answer 1

Given the equation:
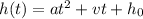`h(t) = at^2+vt+h_0` .....[1]

If t = 0, then h = 0.

Substitute these in [1] we get;

`h(0)=a \cdot (0)^2+v \cdot (0) + h_0`

`0=a \cdot (0)^2+v \cdot (0) + h_0`

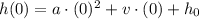
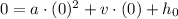
Simplify:

`h_0 = 0`

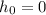
Also, it is given that the acceleration due to gravity (a) =
`-16ft/s^2`

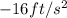
then;

[1] ⇒
`h(t) = -16t^2+vt`

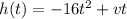
If the ball reaches a maximum height of 25 ft and spends a total of 2.5 s in the air.

⇒ total time = 2.5 s

The height of ball is maximum at t =1.25 s

⇒h(1.25) = 25 ft

we have;

`h(1.25) = -16(1.25)^2 +v(1.25)`

Solve for velocity(v);

`25= -16(1.25)^2 +v(1.25)`

`25 = 1.25(-16(1.25)+v)`

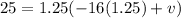
Divide both sides by 1.25 we get;

`20 =-16(1.25)+v`

`20 =-20+v`

Add 20 both sides to an equation we get;

v = 40 ft\s

Therefore, the equation become to models the height of the ball is;

`h(t) = -16t^2+40t`