Answer:
All 3 options A,B,C satisfy.
Explanation:
Given : Max's pet inchworm lives in a cardboard box that has a volume of 80 cubic centimeters.
To find : Which of the following could be the dimensions of Max's box? Choose all answers that apply.
Solution :
The volume of the cardboard is
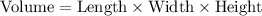
We have given options,
Option A - 2 cm long,5 cm width, 8 cm high
Applying volume formula,
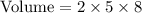
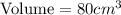
Which is equivalent to Max's pet box.
Option B - 4 cm long,5 cm width, 4 cm high
Applying volume formula,
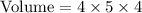
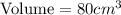
Which is equivalent to Max's pet box.
Option C - 10 cm long,4 cm width, 2 cm high
Applying volume formula,

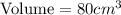
Which is equivalent to Max's pet box.
Therefore, All 3 options satisfying the condition.