Question

Find the range of y = 3/2 cos 4x - 1

I tried it and I got an answer of -1/2 <= y <= 3/2!! But this is not one of the choices!


Choices:

A) -1/2 <= y <= 1/2

B) -2 1/2 <= y <= 1/2

C) -3/2 <= y <=3/2

D) -5 <= y <=3

Answer 1

B.
`-2(1)/(2) \leq y \leq (1)/(2)`

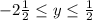
Explanation:

The given trigonometric function is

`f(x)=(3)/(2)cos4x-1`.

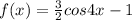The amplitude of this function is
`(3)/(2)`, so under normal circumstances the range is supposed to be

`-(3)/(2) \leq y \leq (3)/(2)`

But the
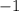`-1` is a downward vertical shift.

Therefore the normal boundaries of the range will shift down one unit to give the range of the transformed function.

We subtract 1 from the lower boundary to get
`-(3)/(2)-1=-2(1)/(2)`

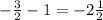
We also subtract 1 from the upper boundary to get
`-frac{3}{2}-1=(1)/(2)`

Hence the range is

`-2(1)/(2) \leq y \leq (1)/(2)`

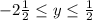
Also see graph