Question

Which domain restriction makes the function f(x) = csc x invertible?

Answer 1

B)
`[-(\pi )/(2),0)` ∪
`(0,(\pi )/(2) ]`

Explanation:

just did the test and this was the right answer for me

Answer 2

the domain after restriction is (-π/2 , + π/2) such that the function f(x)=csc x becomes invertible.

Explanation:

the function f(x) is given by
`f(x)=\csc x`

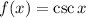
The domain of
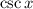`\csc x` is all the real numbers except nπ where n belongs to integers,and range of
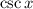`\csc x` is (-∞ , -1] U [1 , + ∞) and it could be seen from the graph that it repeats this value infinte times.

in order to make the function invertible i.e. 1-1 and onto we restrict our domain in such a way that it takes these values exactly once i.e. there is a unique image of each x-value.

hence, the domain after restriction becomes:(-π/2 , + π/2).