Solve sin(x)(sinx +1) = 0

Question

asked Aug 16, 2020 17.8k views

1 Answer

Alex Hart · Answer 1 · 2020-08-22T03:27:53+0000

Answer:

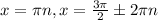
$x=\p \pi n ,x=(3\pi)/(2) \pm 2\pi n$

Explanation:

We want to solve the equation,

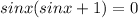
sinx(sin x+1)=0

By the zero product property of multiplication,

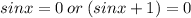
$sinx=0\:or\:(sin x+1)=0$

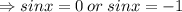
$\Rightarrow sinx=0\:or\:sin x=-1$

If
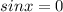sinx=0 , then,
$x=\pi$

The general solution is

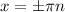
$x=\pm \pi n$

For
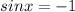sinx=-1 , it means
is either in the third quadrant or fourth quadrant.

So we first solve for,

sinx=1

This implies that,

$x=(\pi)/(2)$

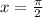
In the third quadrant,

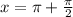
$x=\pi +(\pi)/(2)$

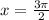
$x=(3\pi)/(2)$

In the fourth quadrant,

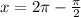
$x=2\pi -(\pi)/(2)$

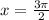
$x=(3\pi)/(2)$

This is a repeated solution.

So the general solution is

If
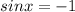sin x=-1 , then
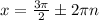
$x=(3\pi)/(2)\pm 2\pi n$

Putting the two solutions together gives

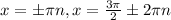$x=\pm \pi n ,x=(3\pi)/(2) \pm 2\pi n$ , where n is an integer

The correct answer is C.