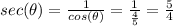Question

Given sin θ = 3/5 what is sec θ?

Answer 1

The correct answer is D 5/4 :)

Answer 2

5/4

Explanation:

To do this you must know that by definition secant is:

`sec(\theta)=(1)/(cos(\theta))`

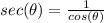
Furthermore:

`sin(\theta)=(opposite)/(hypotenuse)\\\\cos(\theta)=(adjacent)/(hypotenuse)`

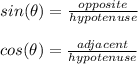
Based on this information we know that 3 = opposite and 5 = hypotenuse. Assuming this is a right triangle we can determine the adjacent side by Pythagorean Theorem.

`c^2=a^2+b^2`

Where c is the hypotenuse, a is adjacent and b is opposite. Therefore,

`c^2=a^2+b^2\\\\a=√(c^2-b^2) \\\\a=√(5^2-3^2) \\\\a=4`

And so the adjacent side of this triangle is 4. Going back to the definition of secant we can now know that:

`sec(\theta)=(1)/(cos(\theta))=(1)/((4)/(5))=(5)/(4)`