Answer: Option C.
Explanation:
1. Apply the Pythagorean Theorem to calculate AB:
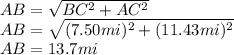
2. Now, you can calculate the angle ∠A as following:
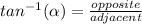
Where:
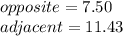
Then:
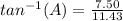
∠
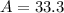 °
°
3. The sum of the interior angles of a triangle is 180°. So, you can find the angle ∠B as following:
∠
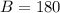 °-∠A-∠C
°-∠A-∠C
∠
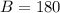 °-
°-
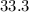 °-
°-
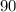 °=
°=
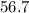 °
°
4. Therefore, the answer is the option c.