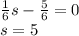Answer:
Explanation:
Given that Miguel is playing a game
The box contains 4 chips, 2 with number 1, and other two differntly numbered as 3 and 5.
OUt of these 4, 2 chips are drawn
P(drawing same number) = 2C2/4C2 =
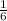
Prob (drawing differnt numbers) = 1-1/6 =

Hence prob of winning 2 dollars =
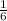
Prob of losing 1 dollar =

b) Expected value = sum of prob x amount won
=
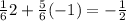
c) Miguel can expect to lose 1/2 dollars for every game he plays
d) If it is to be a fair game expected value =0
i.e. let the amount assigned be s
Then