Question

for the following data set calculate the percentage of data points that fall within one standard deviation of the mean, and compare the result to the expected percentage of a normal distribution. {50,46,54,51,29,52,48,54,47,48}

Answer 1

Answer: 90%;higher than the expected percentage of a normal distribution.

Step-by-step explanation: your welcome

Answer 2

First we need to find the mean and standard deviation of the given data.

The mean and standard deviation are given below:

`Mean=(50+46+54+51+29+52+48+54+47+48)/(10)=(479)/(10)=47.9`

`Standard-deviation=\sqrt{\frac{\sum(x-\bar{x})^2}{n-1} }`

`=\sqrt{((50-47.9)^2+(46-47.9)^2+(54-47.9)^2+...+(48-47.9)^2)/(10-1) }`

`=7.20`

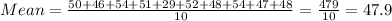
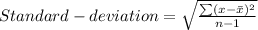
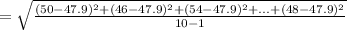
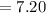
We have:

`\bar{x} \pm s=(47.9 \pm 7.20)`

`=(47.9-7.20, 47.9+7.20)`

`=(40.7, 55.1)`

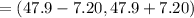
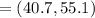
Therefore, the percentage of values that lies within one standard deviation of the mean is:

`(9)/(10) * 100 =90\%`

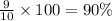
The expected percentage of values within one standard deviation of the mean according to normal distribution is 68%.

Therefore, the observed percentage of values within one standard deviation of the mean is much higher than the expected percentage of a normal distribution.