Answer:
The maximum displacement from the equilibrium position is 9
Explanation:
We are given
equation for the simple harmonic motion equation
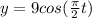
we can use trig formula
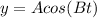
The maximum value of this equation is always A
So, firstly, we will compare and find A
A=9
so,
The maximum displacement from the equilibrium position is 9