Question

Janet scored 200 and 400 points in the first 2 rounds of a computer game.

Michael scores 250 points in the first round. H want to get the same total score as janet.
Which of these will help him find out how many points he need to catch up?
A. 250- 200=p
B.(200+400)-250=p
C.200+400+250=p
D.400-250=p

Answer 1

B

Explanation:

Answer 2

B.
`(200+400)-250=p`

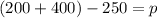
Step-by-step explanation:

Let p be number of points Michael needs to score in 2nd game to catch up.

We have been given that Janet scored 200 and 400 points in the first 2 rounds of a computer game. So the total points scored by Janet in two games will be:
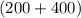`(200+400)` points.

We are also told that Michael had scored 250 points in the first round and he want to get the same total score as Janet.

So we can find the number of points Michael needs to score to catch up Janet by subtracting the number of points scored by Michael in 1st game from total number of points scored by Janet in two games. We can represent this information in an equation as:

`(200+400)-250=p`

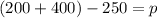
Therefore, the equation
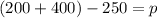`(200+400)-250=p` will help Michael to find the number of points he need to catch up Janet and option B is the correct choice.