Answer:
B)

Explanation:
We are given,
The graph of the parabola opens downwards.
This means that the leading co-efficient of the function will be negative.
So, options C and D are not possible.
Moreover, it is given that the graph cuts x-axis near
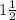 i.e.
i.e.
 = 1.5 and
= 1.5 and
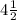 i.e.
i.e.
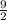 = 4.5.
= 4.5.
i.e. At y=0, the value of x is near
 and
and
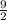 .
.
A. So, in
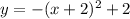 , we put y =0.
, we put y =0.
i.e.
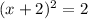
i.e.
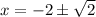
i.e. x = 0.68 and x = 3.41
We see that this does not crosses the x-axis at the given points.
So, option A is wrong.
B. Also, in
 , we put y =0.
, we put y =0.
i.e.

i.e.
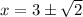
i.e. x = 1.68 and x = 4.41.
Thus, this equation cuts the x-axis near the given points i.e. 1.5 and 4.5.
Hence, the equation of the given graph is
 .
.