 , so I assume you mean "find
, so I assume you mean "find
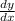 ".
".
We can rewrite this as an implicit equation to avoid using too much of the chain rule, namely
![y = \sqrt[3]{(e^x (x+1))/(x^2+1)} \implies (x^2+1) y^3 = e^x (x+1)](https://img.qammunity.org/2023/formulas/mathematics/high-school/q2havl6htc5y2ay2yds10h28c9g0nxewjp.png)
Differentiate both sides with respect to
 using the product and chain rules.
using the product and chain rules.
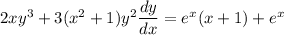

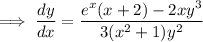
Now substitute the original expression for
 .
.
![(dy)/(dx) = \frac{e^x (x+2) - 2x \left(\sqrt[3]{(e^x(x+1))/(x^2+1)}\right)^3}{3(x^2+1) \left(\sqrt[3]{(e^x(x+1))/(x^2+1)}\right)^2}](https://img.qammunity.org/2023/formulas/mathematics/high-school/wanjhhkwm315g1cl0reglimn38zoo3tkv1.png)
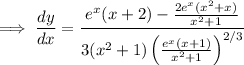
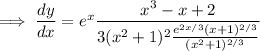
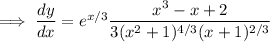
Now, since
![y = \sqrt[3]{(e^x (x+1))/(x^2+1)} = (e^(x/3) (x+1)^(1/3))/((x^2+1)^(1/3))](https://img.qammunity.org/2023/formulas/mathematics/high-school/kxn7qcnexjw2ji895ttx4ygd5yb1zn7ivz.png)
we can write
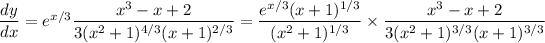

Focusing on the rational expression in
 , we have the partial fraction expansion
, we have the partial fraction expansion

where we have the constant term on the right side because both the numerator and denominator have degree 3.
Writing everything with a common denominator and equating the numerators leads to

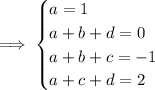
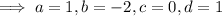
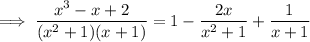
and it follows that
