Answer:
Part (A) The wrong step is step 3
Part (B) The correct option is D) x ≥ −1/3
Explanation:
Consider the provided inequality.
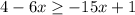
Step 1. subtract 1 from both the sides.
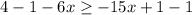
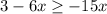
Step 2. Add 6x both sides.
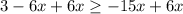
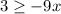
Step 3. Divide both sides by -9 and change the sign of inequality.
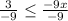
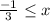
Part (A) The wrong step is step 3
Part (B)
From the above calculation the solution of the inequality is
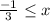
Hence, the correct option is D) x ≥ −1/3