Question

The graphs of the two lines 4x=3y+23 and 4y+3x= -19 A. do not intersect. B. are identical C. intersect at (-2,5) D.are perpendicular

Answer 1

The correct option is D.

Explanation:

The given equations are

`4x=3y+23`

`4y+3x=-19`

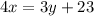
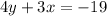
The slope intercept form of a line is

`y=mx+b`

where, m is slope and b is y-intercept.

Rewrite the given equations is the slope intercept form.

`y=(4)/(3)x-(23)/(3)`

`y=-(3)/(4)x-\fra{19}{4}`

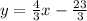
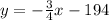
Therefore the slope of first line is
`(4)/(3)` and the slope of second line is
`-(3)/(4)`.

`m_1* m_2=(4)/(3)* =-(3)/(4)=-1`

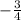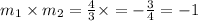
Since the product of slopes of two perpendicular lines is -1, therefore we can say that both lines are perpendicular to each other. Option D is correct.