Question

Find the solution set of this inequality|10x+20| ≤10

Answer 1

solution is

[-3,-1]

Explanation:

we are given

`|10x+20|\leq 10`

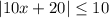
Firstly, we will find critical values

so, let's assume it is equal

`|10x+20|= 10`

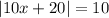
now, we can break absolute sign

For
`|10x+20|= -(10x+20)`:

`-(10x+20)= 10`

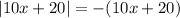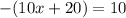
we can solve for x

`-10x-20= 10`

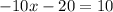
Add both sides by 20

`-10x-20+20= 10+20`

`-10x= 30`

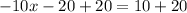
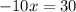
Divide both sides by -10

and we get

`x=-3`

For
`|10x+20|= (10x+20)`:

`(10x+20)= 10`

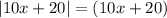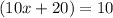
we can solve for x

`10x+20= 10`

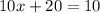
Subtract both sides by 20

`10x+20-20= 10-20`

`10x= -10`

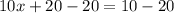
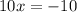
Divide both sides by 10

and we get

`x=-1`

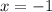
so, critical values are

`x=-3`

`x=-1`

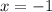
now, we can draw a number line and locate these values

and then we can check inequality on each intervals

For
`(-\infty,-3)`:

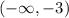We can select any random value from this interval and plug that in inequality

and we get

we can plug x=-5

`|10* -5+20|\leq 10`

`|-50+20|\leq 10`

`30\leq 10`

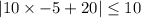
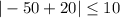
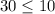
so, this is FALSE

For
`[-3,-1]`:

We can select any random value from this interval and plug that in inequality

and we get

we can plug x=-2

`|10* -2+20|\leq 10`

`|-20+20|\leq 10`

`0\leq 10`

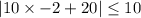
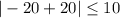
so, this is TRUE

For
`(-1,\infty)`:

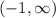We can select any random value from this interval and plug that in inequality

and we get

we can plug x=0

`|10* 0+20|\leq 10`

`|0+20|\leq 10`

`20\leq 10`

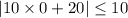
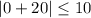
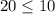
so, this is FALSE

so, solution is

[-3,-1]