Question

Which selection describes the relationship?

Answer 1

The correct answer option is decreasing and linear.

Explanation:

We are given a set of corresponding values for x and y and we are to determine whether which of the given answer options describe the relationship.

We can find the slope using these points and compare the values we get:

`m_1=(-13-(-8))/(4-3) =-5`

`m_2=(-8-(-3))/(3-2) =-5`

`m_3=(-3-2)/(2-1) =-5`

The slope is constant and negative. Therefore, the correct answer option is decreasing and linear.

Answer 2

The correct option is 3.

Explanation:

From the given table it is noticed that function is passing through the points (1,2), (2,-3), (3,-8) and (4,-13).

The slope of the function on first two point (1,2) and (2,-3) is,

`m_1=(-3-2)/(2-1)=(-5)/(1)=-5`

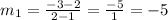
The slope of the function on first two point (2,-3) and (3,-8) is,

`m_2=(-8-(-3))/(3-1)=(-5)/(1)=-5`

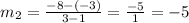
The slope of the function on last two point (3,-8) and (4,-13) is,

`m_3=(-13+8)/(4-3)=(-5)/(1)=-5`

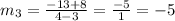
The slope of function is same form all points.

Since the slope or rate of change is constant and negative, therefore the function is decreasing and linear. Option 3 is correct.