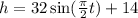Answer:
Required model is
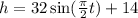
Explanation:
Given : An iron ball is bobbing up and down on the end of a spring. The maximum height of the ball is 46 inches and its minimum height is 18 inches. It takes the ball 2 seconds to go from its maximum height to its minimum height.
To find : Which model best represents the height, h, of the ball after t seconds?
Solution :
According to question,
The height function must be trigonometric in nature.
So, we can use formula,
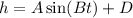
Now, We calculate A,B and D
1) Maximum height 46 inch
Minimum height =18 inch
Average height is A
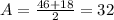
2) It takes the ball 2 seconds to go from its maximum height to its minimum height
So, half of time period is 2 sec
i.e,
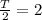
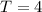
Period is B
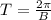
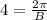
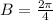
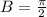
3) D is the midline
So, Max=46 and min=18
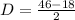
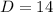
Substituting all the values,
A=32 , D=14 ,
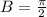
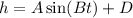
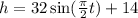
Therefore, Required model is